第一讲：方程组的几何解释

我们从求解线性方程组来开始这门课，从一个普通的例子讲起：方程组有 $2$ 个未知数，一共有 $2$ 个方程，分别来看方程组的“行图像”和“列图像”。

有方程组 ${\begin{cases} 2 x & - y & = 0 \\ - x & + 2 y & = 3 \end{cases}$ ，写作矩阵形式有 $[\begin{matrix} 2 & - 1 \\ - 1 & 2 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}] = [\begin{matrix} 0 \\ 3 \end{matrix}]$ ，通常我们把第一个矩阵称为系数矩阵 $A$ ，将第二个矩阵称为向量 $x$ ，将第三个矩阵称为向量 $b$ ，于是线性方程组可以表示为 $A x = b$ 。

我们来看行图像，即直角坐标系中的图像：

python

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

x = [-2, 2, -2, 2]
y = [-4, 4, 0.5, 2.5]

fig = plt.figure()
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')

plt.plot(x[:2], y[:2], x[2:], y[2:])

plt.draw()

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

x = [-2, 2, -2, 2]
y = [-4, 4, 0.5, 2.5]

fig = plt.figure()
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')

plt.plot(x[:2], y[:2], x[2:], y[2:])

plt.draw()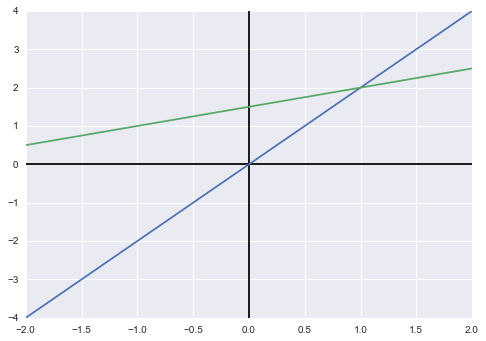

png

python

plt.close(fig)

plt.close(fig)

上图是我们都很熟悉的直角坐标系中两直线相交的情况，接下来我们按列观察方程组 $x [\begin{matrix} 2 \\ - 1 \end{matrix}] + y [\begin{matrix} - 1 \\ 2 \end{matrix}] = [\begin{matrix} 0 \\ 3 \end{matrix}]$ （我们把第一个向量称作 $c o l_{1}$ ，第二个向量称作 $c o l_{2}$ ，以表示第一列向量和第二列向量），要使得式子成立，需要第一个向量加上两倍的第二个向量，即 $1 [\begin{matrix} 2 \\ - 1 \end{matrix}] + 2 [\begin{matrix} - 1 \\ 2 \end{matrix}] = [\begin{matrix} 0 \\ 3 \end{matrix}]$ 。

现在来看列图像，在二维平面上画出上面的列向量：

python

from functools import partial

fig = plt.figure()
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
ax = plt.gca()
ax.set_xlim(-2.5, 2.5)
ax.set_ylim(-3, 4)

arrow_vector = partial(plt.arrow, width=0.01, head_width=0.1, head_length=0.2, length_includes_head=True)

arrow_vector(0, 0, 2, -1, color='g')
arrow_vector(0, 0, -1, 2, color='c')
arrow_vector(2, -1, -2, 4, color='b')
arrow_vector(0, 0, 0, 3, width=0.05, color='r')

plt.draw()

from functools import partial

fig = plt.figure()
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
ax = plt.gca()
ax.set_xlim(-2.5, 2.5)
ax.set_ylim(-3, 4)

arrow_vector = partial(plt.arrow, width=0.01, head_width=0.1, head_length=0.2, length_includes_head=True)

arrow_vector(0, 0, 2, -1, color='g')
arrow_vector(0, 0, -1, 2, color='c')
arrow_vector(2, -1, -2, 4, color='b')
arrow_vector(0, 0, 0, 3, width=0.05, color='r')

plt.draw()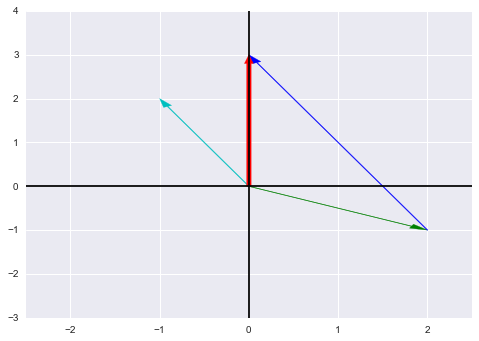

png

python

plt.close(fig)

plt.close(fig)

如图，绿向量 $c o l_{1}$ 与蓝向量（两倍的蓝绿向量 $c o l_{2}$ ）合成红向量 $b$ 。

接着，我们继续观察 $x [\begin{matrix} 2 \\ - 1 \end{matrix}] + y [\begin{matrix} - 1 \\ 2 \end{matrix}] = [\begin{matrix} 0 \\ 3 \end{matrix}]$ ， $c o l_{1}, c o l_{2}$ 的某种线性组合得到了向量 $b$ ，那么 $c o l_{1}, c o l_{2}$ 的所有线性组合能够得到什么结果？它们将铺满整个平面。

下面进入三个未知数的方程组： ${\begin{cases} 2 x & - y & = 0 \\ - x & + 2 y & - z & = - 1 \\ - 3 y & + 4 z & = 4 \end{cases}$ ，写作矩阵形式 $A = [\begin{matrix} 2 & - 1 & 0 \\ - 1 & 2 & - 1 \\ 0 & - 3 & 4 \end{matrix}], b = [\begin{matrix} 0 \\ - 1 \\ 4 \end{matrix}]$ 。

在三维直角坐标系中，每一个方程将确定一个平面，而例子中的三个平面会相交于一点，这个点就是方程组的解。

同样的，将方程组写成列向量的线性组合，观察列图像： $x [\begin{matrix} 2 \\ - 1 \\ 0 \end{matrix}] + y [\begin{matrix} - 1 \\ 2 \\ - 3 \end{matrix}] + z [\begin{matrix} 0 \\ - 1 \\ 4 \end{matrix}] = [\begin{matrix} 0 \\ - 1 \\ 4 \end{matrix}]$ 。已知教授特意安排的例子中最后一个列向量恰巧等于等式右边的 $b$ 向量，所以我们需要的线性组合为 $x = 0, y = 0, z = 1$ 。假设我们令 $b = [\begin{matrix} 1 \\ 1 \\ - 3 \end{matrix}]$ ，则需要的线性组合为 $x = 1, y = 1, z = 0$ 。

我们并不能总是这么轻易的求出正确的线性组合，所以下一讲将介绍消元法——一种线性方程组的系统性解法。

现在，我们需要考虑，对于任意的 $b$ ，是否都能求解 $A x = b$ ？用列向量线性组合的观点阐述就是，列向量的线性组合能否覆盖整个三维向量空间？对上面这个例子，答案是肯定的，这个例子中的 $A$ 是我们喜欢的矩阵类型，但是对另一些矩阵，答案是否定的。那么在什么情况下，三个向量的线性组合得不到 $b$ ？

——如果三个向量在同一个平面上，问题就出现了——那么他们的线性组合也一定都在这个平面上。举个例子，比如 $c o l_{3} = c o l_{1} + c o l_{2}$ ，那么不管怎么组合，这三个向量的结果都逃不出这个平面，因此当 $b$ 在平面内，方程组有解，而当 $b$ 不在平面内，这三个列向量就无法构造出 $b$ 。在后面的课程中，我们会了解到这种情形称为奇异、矩阵不可逆。

下面我们推广到九维空间，每个方程有九个未知数，共九个方程，此时已经无法从坐标图像中描述问题了，但是我们依然可以从求九维列向量线性组合的角度解决问题，仍然是上面的问题，是否总能得到 $b$ ？当然这仍取决于这九个向量，如果我们取一些并不相互独立的向量，则答案是否定的，比如取了九列但其实只相当于八列，有一列毫无贡献（这一列是前面列的某种线性组合），则会有一部分 $b$ 无法求得。

接下来介绍方程的矩阵形式 $A x = b$ ，这是一种乘法运算，举个例子，取 $A = [\begin{matrix} 2 & 5 \\ 1 & 3 \end{matrix}], x = [\begin{matrix} 1 \\ 2 \end{matrix}]$ ，来看如何计算矩阵乘以向量：

我们依然使用列向量线性组合的方式，一次计算一列， $[\begin{matrix} 2 & 5 \\ 1 & 3 \end{matrix}] [\begin{matrix} 1 \\ 2 \end{matrix}] = 1 [\begin{matrix} 2 \\ 1 \end{matrix}] + 2 [\begin{matrix} 5 \\ 3 \end{matrix}] = [\begin{matrix} 12 \\ 7 \end{matrix}]$
另一种方法，使用向量内积，矩阵第一行向量点乘 $x$ 向量 $[\begin{matrix} 2 & 5 \end{matrix}] \cdot {[\begin{matrix} 1 & 2 \end{matrix}]}^{T} = 12, [\begin{matrix} 1 & 3 \end{matrix}] \cdot {[\begin{matrix} 1 & 2 \end{matrix}]}^{T} = 7$ 。

教授建议使用第一种方法，将 $A x$ 看做 $A$ 列向量的线性组合。

第一讲：方程组的几何解释 ​

第一讲：方程组的几何解释