第三十五讲：期末复习 ​

依然是从以往的试题入手复习知识点。

1. 已知$m\times n$矩阵$A$，有$Ax=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$无解；$Ax=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$仅有唯一解，求关于$m,n,rank(A)$的信息。

   首先，最容易判断的是$m=3$；而根据第一个条件可知，矩阵不满秩，有$r<m$；根据第二个条件可知，零空间仅有零向量，也就是矩阵消元后没有自由变量，列向量线性无关，所以有$r=n$。

   综上，有$m=3>n=r$。

   根据所求写出一个矩阵$A$的特例：$A=\left[\begin{array}{cc}0& 0\\ 1& 0\\ 0& 1\end{array}\right]$。

   $det{A}^{T}A\stackrel{?}{=}detA{A}^T$：不相等，因为$A^{T}A$可逆而$A{A}^T$不可逆，所以行列式不相等。（但是对于方阵，$detAB=detBA$恒成立。）

   *$A^{T}A$可逆吗？*是，因为$r=n$，矩阵列向量线性无关，即列满秩。

   *$A{A}^T$正定吗？*否，因为$A{A}^T$是$3\times n$矩阵与$n\times 3$矩阵之积，是一个三阶方阵，而$A{A}^T$秩为$2$，所以不是正定矩阵。（不过$A{A}^T$一定是半正定矩阵。）

   求证$A^{T}y=c$至少有一个解：因为$A$的列向量线性无关，所以$A^T$的行向量线性无关，消元后每行都有主元，且总有自由变量，所以零空间中有非零向量，零空间维数是$m-r$（可以直接从$\dim N\left(A^T\right)=m-r$得到结论）。

2. 设$A=[v_1{v}_2{v}_3]$，对于$Ax=v_1-v_2+v_3$，求$x$。

   按列计算矩阵相乘，有$x=\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]$。

   *若Ax=v_1-v_2+v_3=0，则解是唯一的吗？为什么。*如果解释唯一的，则零空间中只有零向量，而在此例中$x=\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]$就在零空间中，所以解不唯一。

   *若$v_1,v_2,v_3$是标准正交向量，那么怎样的线性组合$c_1{v}_1+c_2{v}_2$能够最接近$v_3$？*此问是考察投影概念，由于是正交向量，所以只有$0$向量最接近$v_3$。

3. 矩阵$A=\left[\begin{array}{ccc}.2& .4& .3\\ .4& .2& .3\\ .4& .4& .4\end{array}\right]$，求稳态。

   这是个马尔科夫矩阵，前两之和为第三列的两倍，奇异矩阵总有一个特征值为$0$，而马尔科夫矩阵总有一个特征值为$1$，剩下一个特征值从矩阵的迹得知为$-.2$。

   再看马尔科夫过程，设从$u(0)$开始，$u_k=A^k{u}_0,u_0=\left[\begin{array}{c}0\\ 10\\ 0\end{array}\right]$。先代入特征值${\lambda }_1=0,{\lambda }_2=1,{\lambda }_3=-.2$查看稳态$u_k=c_1{\lambda }_1^k{x}_1+c_2{\lambda }_2^k{x}_2+c_3{\lambda }_3^k{x}_3$，当$k\to \mathrm{\infty }$，第一项与第三项都会消失，剩下$u_{\mathrm{\infty }}=c_2{x}_2$。

   到这里我们只需求出${\lambda }_2$对应的特征向量即可，带入特征值求解$(A-I)x=0$，有$\left[\begin{array}{ccc}-.8& .4& .3\\ .4& -.8& .3\\ .4& .4& -.6\end{array}\right]\left[\begin{array}{c}?\\ ?\\ ?\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$，可以消元得，也可以直接观察得到$x_2=\left[\begin{array}{c}3\\ 3\\ 4\end{array}\right]$。

   剩下就是求$c_2$了，可以通过$u_0$一一解出每个系数，但是这就需要解出每一个特征值。另一种方法，我们可以通过马尔科夫矩阵的特性知道，对于马尔科夫过程的每一个$u_k$都有其分量之和与初始值分量之和相等，所以对于$x_2=\left[\begin{array}{c}3\\ 3\\ 4\end{array}\right]$，有$c_2=1$。所以最终结果是$u_{\mathrm{\infty }}=\left[\begin{array}{c}3\\ 3\\ 4\end{array}\right]$。

4. 对于二阶方阵，回答以下问题：

   求投影在直线$a=\left[\begin{array}{c}4\\ -3\end{array}\right]$上的投影矩阵：应为$P=\frac{a{a}^T}{a^{T}a}$。

   已知特征值${\lambda }_1=2,x_1=\left[\begin{array}{c}1\\ 2\end{array}\right]{\lambda }_2=3,x_2=\left[\begin{array}{c}2\\ 1\end{array}\right]$求原矩阵$A$：从对角化公式得$A=S\mathrm{\Lambda }{S}^{-1}=\left[\begin{array}{cc}1& 2\\ 2& 1\end{array}\right]\left[\begin{array}{cc}0& 0\\ 0& 3\end{array}\right]{\left[\begin{array}{cc}1& 2\\ 2& 1\end{array}\right]}^{-1}$，解之即可。

   $A$是一个实矩阵，且对任意矩阵$B$，$A$都不能分解成$A=B^{T}B$，给出$A$的一个例子：我们知道$B^{T}B$是对称的，所以给出一个非对称矩阵即可。 矩阵$A$有正交的特征向量，但不是对称的，给出一个$A$的例子：我们在三十三讲提到过，反对称矩阵，因为满足$A{A}^T=A^{T}A$而同样具有正交的特征向量，所以有$A=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$或旋转矩阵$\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$，这些矩阵都具有复数域上的正交特征向量组。

5. 最小二乘问题，因为时间的关系直接写出计算式和答案，$\left[\begin{array}{cc}1& 0\\ 1& 1\\ 1& 2\end{array}\right]\left[\begin{array}{c}C\\ D\end{array}\right]=\left[\begin{array}{c}3\\ 4\\ 1\end{array}\right](Ax=b)$，解得$\left[\begin{array}{c}\hat{C}\\ \hat{D}\end{array}\right]=\left[\begin{array}{c}\frac{11}{3}\\ -1\end{array}\right]$。

   求投影后的向量$p$：向量$p$就是向量$b$在矩阵$A$列空间中的投影，所以$p=\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 1& 1\\ 1& 2\end{array}\right]\left[\begin{array}{c}\hat{C}\\ \hat{D}\end{array}\right]$。

   求拟合直线的图像：$x=0,1,2$时$y=p_1,p_2,p_2$所在的直线的图像，$y=\hat{C}+\hat{D}x$即$y=\frac{11}{3}-x$。

%matplotlib inline
import matplotlib.pyplot as plt
from sklearn import linear_model
import numpy as np
import pandas as pd
import seaborn as sns

x = np.array([0, 1, 2]).reshape((-1,1))
y = np.array([3, 4, 1]).reshape((-1,1))
predict_line = np.array([-1, 4]).reshape((-1,1))

regr = linear_model.LinearRegression()
regr.fit(x, y)
ey = regr.predict(x)

fig = plt.figure()
plt.axis('equal')
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')

plt.scatter(x, y, c='r')
plt.scatter(x, regr.predict(x), s=20, c='b')
plt.plot(predict_line, regr.predict(predict_line), c='g', lw='1')
[ plt.plot([x[i], x[i]], [y[i], ey[i]], 'r', lw='1') for i in range(len(x))]

plt.draw()

%matplotlib inline
import matplotlib.pyplot as plt
from sklearn import linear_model
import numpy as np
import pandas as pd
import seaborn as sns

x = np.array([0, 1, 2]).reshape((-1,1))
y = np.array([3, 4, 1]).reshape((-1,1))
predict_line = np.array([-1, 4]).reshape((-1,1))

regr = linear_model.LinearRegression()
regr.fit(x, y)
ey = regr.predict(x)

fig = plt.figure()
plt.axis('equal')
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')

plt.scatter(x, y, c='r')
plt.scatter(x, regr.predict(x), s=20, c='b')
plt.plot(predict_line, regr.predict(predict_line), c='g', lw='1')
[ plt.plot([x[i], x[i]], [y[i], ey[i]], 'r', lw='1') for i in range(len(x))]

plt.draw()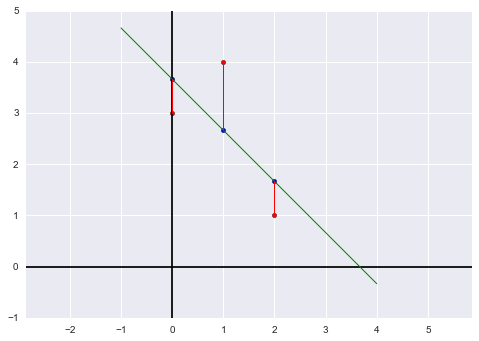

plt.close(fig)

plt.close(fig)

• 接上面的题目

  求一个向量$b$使得最小二乘求得的$\left[\begin{array}{c}\hat{C}\\ \hat{D}\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$：我们知道最小二乘求出的向量$\left[\begin{array}{c}\hat{C}\\ \hat{D}\end{array}\right]$使得$A$列向量的线性组合最接近$b$向量（即$b$在$A$列空间中的投影），如果这个线性组合为$0$向量（即投影为$0$），则$b$向量与$A$的列空间正交，所以可以取$b=\left[\begin{array}{c}1\\ -2\\ 1\end{array}\right]$同时正交于$A$的两个列向量。

MIT线性代数的全部课程到此结束 ​